ERGODIQUE (THÉORIE)

ERGODIQUE (THÉORIE)

Ergodique vient du mot grec 﨎福塚礼益 qui signifie travail. C’est en effet d’un problème de mécanique que la théorie ergodique est issue. À l’origine se trouve une hypothèse de la théorie cinétique des gaz, audacieusement posée par L. Boltzmann en 1885, qui permettait aux physiciens de résoudre une difficulté liée à l’étude des systèmes mécaniques à un très grand nombre de particules. L’importance de cette hypothèse, confirmée expérimentalement dans de nombreux cas, conduisit les mécaniciens à en chercher une justification théorique et ce sont les diverses tentatives faites dans cette voie qui marquent les débuts de la théorie ergodique.

Après les résultats fondamentaux, obtenus par J. von Neumann et G. D. Birkhoff en 1931 à quelques semaines d’intervalle, la théorie ergodique s’est développée au sein de la mathématique dans des directions diverses: analyse fonctionnelle et théorie des groupes; calcul des probabilités et plus précisément processus markoviens; théorie de l’information, etc. Les méthodes ergodiques ont permis d’exposer différemment certains problèmes et de donner des prolongements nouveaux à ces branches de la mathématique. L’étude de la théorie ergodique suppose la connaissance de la théorie de la mesure ^{[cf. INTÉGRATION ET MESURE]}.

1. Le modèle de Poincaré et l’hypothèse ergodique

Pour expliquer l’hypothèse ergodique, il est commode d’avoir recours à un modèle très simple imaginé par H. Poincaré. Supposons un liquide en mouvement stationnaire dans un récipient 行 de forme invariable et complètement rempli. Si une molécule du liquide occupe la position 諸⁰ à l’instant 0 et 諸^t à l’instant t , on peut décrire le passage de l’instant 0 à l’instant t et, plus généralement, de l’instant s à l’instant s + t , au moyen d’une transformation ponctuelle ^t opérant dans 行, pour laquelle:

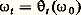et:

et cela pour toutes les molécules de liquide. Il va de soi que ces transformations forment un groupe, c’est-à-dire que:

quels que soient s , t 捻 R; ou bien, si l’on se désintéresse du passé, un semi-groupe en ne considérant la condition (1) que pour des valeurs positives ou nulles s et t . Pour t = 0, ⁰ désigne la transformation identique de 行. On peut envisager une simplification supplémentaire en se limitant aux instants discrets..., 漣 2, 漣 1, 0, 1, 2, ... et, en posant ¹ = , se ramener à l’étude du groupe G à un générateur :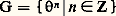

ou bien du semi-groupe:

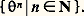En outre, l’incompressibilité du liquide amène à poser la condition suivante: Si E est un volume partiel de 行 et si:

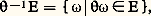alors les mesures de E et de ^-1E sont égales; autrement dit, la transformation conserve la mesure. Pour un point donné 諸 捻 行, l’ensemble:

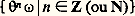est appelé trajectoire de 諸. On dit qu’un point 諸 est topologiquement infiniment récurrent si tout voisinage de ce point possède une infinité de points de sa trajectoire. On peut alors énoncer le théorème de récurrence qui peut être considéré comme le premier théorème ergodique et qui fut établi par H. Poincaré en 1890.

Théorème de Poincaré . Presque tout point de 行 est topologiquement infiniment récurrent.

En vérité, cela n’est pas exactement l’énoncé donné par le célèbre géomètre qui ne pouvait pas faire usage à cette époque de la théorie de la mesure de Lebesgue, théorie qui permit quelques années plus tard de prouver le théorème de Poincaré.

Revenant au problème général, considérons un système mécanique 崙 constitué par N particules. L’état de 崙 à chaque instant est déterminé par la connaissance des 3 N coordonnées des particules et des 3 N composantes de leurs vitesses. Ces états peuvent ainsi être représentés par des points 諸 de l’espace R^6N appelé espace de phase. Il peut être aussi plus commode de substituer à ces 6 N coordonnées 6 N autres paramètres qu’on ne précisera pas ici. Le système 崙 évolue sous l’action de forces extérieures et des actions mutuelles des particules, et cette évolution est régie par un système d’équations différentielles qui permet de déterminer à partir d’un état initial 諸⁰ l’état 諸^t du système à l’instant t . Si 崙 est conservatif, les trajectoires des points 諸 sont portées par des variétés plongées dans R^6N et chacune de celles-ci correspond à une valeur constante de l’énergie de 崙, ce qui explique l’emploi du terme ergodique. L’une quelconque de ces variétés sera pour nous le récipient 行 du modèle de Poincaré. L’invariance de la mesure, lorsque les paramètres décrivant l’état de 崙 sont convenablement choisis, est assurée par un résultat général dû à Liouville. Le physicien qui observe l’évolution du système s’intéresse à des mesures portant sur les valeurs de fonctions de l’état de 崙 (observables). Soit f l’une d’elles, f : 行R. Si l’on tient compte d’une part du grand nombre de particules et du fait que, dans un intervalle de temps très petit pris pour unité, se produit un nombre très élevé de microphénomènes (collision de particules, etc.), si l’on tient compte d’autre part de la durée qu’exige une mesure, on s’aperçoit que le physicien ne peut pas comparer ses mesures aux valeurs théoriques instantanées f ( 諸) mais plutôt aux moyennes temporelles:

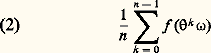portant sur n instants consécutifs 0, 1, 2, ..., n 漣 1 et cela pour de très grandes valeurs de n . Ensuite, en supposant même que l’état initial 諸 soit parfaitement connu, la détermination des états successifs 諸, ² 諸, ..., ^n-1 諸 exigerait l’intégration du système différentiel mentionné plus haut, calcul pratiquement impossible à effectuer. Il faut donc imaginer un autre moyen d’atteindre les quantités théoriques (2) et c’est là qu’intervient l’hypothèse ergodique. Cette hypothèse postule l’égalité des moyennes de phase:

des moyennes (2) pour n assez grand, 行 étant la variété associée aux données de l’expérience.

2. Les théorèmes de G. D. Birkhoff et de J. von Neumann

On va maintenant formaliser le problème ergodique. On se donne un espace compact 行 et une mesure de Radon positive m sur 行 (cf. INTÉGRATION ET MESURE; on peut se placer dans des situations plus générales, mais on n’a pas jugé utile de le faire ici), qui est aussi une probabilité m ( 行) = 1 (cf. calcul des PROBABILITÉS). On se donne aussi une transformation mesurable : 行行 et on suppose que conserve la mesure, c’est-à-dire que vérifie la condition: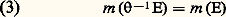

pour tout ensemble mesurable E. Cette condition entraîne que ^-1E est négligeable si E est négligeable, c’est-à-dire m (E) = 0.

Théorème de Birkhoff . Soit f une fonction complexe et intégrable sur 行; la suite des moyennes de Cesaro:

converge presque partout sur 行 vers une fonction intégrable face="EU Caron" キ ; cette fonction face="EU Caron" キ est -invariante (c’est-à-dire face="EU Caron" キ = face="EU Caron" キ 獵 ) et enfin: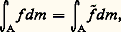

quel que soit l’ensemble mesurable A invariant, c’est-à-dire tel que A = ^-1A.

Dans le cas particulier où la condition (E) suivante est satisfaite: les seuls ensembles invariants sont modulo les ensembles négligeables, l’ensemble 行 et l’ensemble vide, les fonctions invariantes sont les fonctions constantes presque partout (p.p.), et le théorème de Birkhoff donne l’égalité:

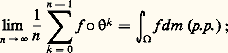autrement dit le système ( 行, m , ) vérifie l’hypothèse ergodique si la condition (E) est remplie. On dit dans ce cas que est transitivement métrique ou encore que est ergodique.

Quelques semaines avant que G. D. Birkhoff eût donné son résultat, J. von Neumann avait établi le théorème suivant en faisant les mêmes hypothèses que pour le théorème de Birkhoff.

Théorème de von Neumann. Soit f une fonction complexe sur 行, de carré intégrable; la suite des fonctions:

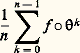converge en moyenne quadratique vers une fonction face="EU Caron" キ de carré intégrable et -invariante; autrement dit:

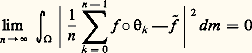et:

Il n’est pas question de donner ici les démonstrations de ces théorèmes, mais il est utile d’ajouter quelques indications sur ces preuves pour montrer en particulier les liens existant entre la théorie ergodique et l’analyse fonctionnelle.

Dans ces théorèmes intervient une transformation agissant non pas sur les points de 行 mais plutôt sur les fonctions définies sur 行. Il s’agit de l’application: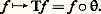

Pour éviter des difficultés techniques, on ne distinguera pas des fonctions égales presque partout; et, d’ailleurs, l’hypothèse d’invariance de la mesure entraîne que, si f est négligeable, c’est-à-dire

f 獵 l’est aussi.

Cela posé, soit L^p l’espace des fonctions complexes sur 行 de puissances p -ièmes intégrables: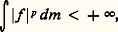

p étant un nombre réel donné 1 諒 p 麗 + 秊. On sait que L² est muni d’une structure d’espace de Hilbert (cf. espace de HILBERT) où le produit hermitien de deux éléments f ¹ et f ² est défini par: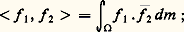

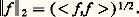f ² est la conjuguée complexe de f ² et la norme d’un élément f est:

Alors il est facile de voir que T est un opérateur linéaire et unitaire sur L². Cela étant, et sans entrer dans les détails, la démonstration du théorème de von Neumann repose sur le fait qu’il existe dans L² deux sous-espaces fermés et orthogonaux 琉 et 流 tels que tout f 捻 L² s’écrive d’une seule manière: f = g + h , avec g 捻 溜 et h 捻 流, où 溜 est le sous-espace des invariants (g 捻 溜 沈 g = Tg ) et 流 est l’adhérence du sous-espace image de I 漣 T.

On ne dira rien de la preuve donnée par Birkhoff de son théorème, mais on donnera une indication sur la démonstration proposée par Yosida et Kakutani. Elle est fondée sur le lemme suivant, nommé par ces auteurs «théorème ergodique maximal».

Soit f 捻 L¹ et E l’ensemble des 諸 pour lesquels l’une au moins des sommes:

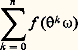est positive; alors:

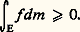Illustrons ce qui précède par deux exemples.

a ) 行 est le tore à une dimension, 行 = R/Z. L’application est définie par 諸 = 諸 + a où a est la classe d’équivalence d’un nombre irrationnel. La mesure m sur 行 est induite par la mesure de Lebesgue sur R. On peut voir facilement ici que conserve la mesure et que est ergodique. On a ainsi:

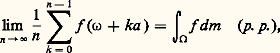quel que soit f 捻 L¹. Ce résultat avait été

démontré directement par Khintchine sans utiliser le théorème de Birkhoff.

b ) 行 est l’intervalle [0, 1] muni de la mesure de Lebesgue. Chaque réel 諸 捻 [0, 1] s’écrit dans le système décimal, au moins d’une manière, 諸 = 0, a ¹a ²a ³ ... où les a ⁱ sont des entiers compris entre 0 et 9. Posons alors:

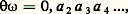en observant que, dans tous les cas, 諸 est bien défini par la donnée de 諸. Il est moins facile ici de vérifier que conserve la mesure et que est ergodique. Admettons-le et prenons f égale à la fonction caractéristique de l’intervalle [q /10, q /10 + 1/10[, avec q 捻0, 1, 2, ..., 8.

On a f ( 諸) = 1, si a ¹ = q ou si a ¹ = q 漣 1 et a ² = a ³ = ... = 9. Le théorème de Birkhoff affirme, dans ces conditions, que:

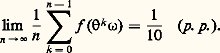Ce résultat, découvert par É. Borel, exprime que, pour presque tout réel x , chaque chiffre admet dans la suite des décimales du nombre x la même fréquence limite 1/10.

3. Propriétés de mélange

Revenons au modèle de Poincaré et supposons que le liquide enfermé dans le récipient 行 soit, suivant une image de Halmos, un mélange de vermouth et de gin dans les proportions de 9/10 de gin et 1/10 de vermouth. Le récipient 行 est un shaker que l’on agite pour confectionner un cocktail. Chaque mouvement d’agitation du shaker s’effectue aux instants 1, 2, ..., n , ... Si B est la partie de 行 occupée initialement par le vermouth, alors, pour toute autre partie mesurable A du shaker, le rapport entre la quantité de vermouth contenue dans A et la quantité totale de vermouth est, à l’instant n ,

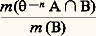ou encore, en désignant par 1^A la fonction caractéristique de l’ensemble A,

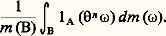La moyenne arithmétique de ces rapports pris aux instants 0, 1, ..., n 漣 1 est donc:

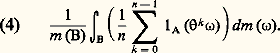On suppose toujours m ( 行) = 1. Si est ergodique, la suite (4) converge vers m (A). Autrement dit, en moyenne, la suite:

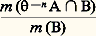converge vers m (A). Cela est, bien entendu, réalisé a fortiori si:

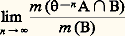condition qui exprime qu’après un temps assez long toute partie telle que A contient la même proportion de gin et de vermouth qui se trouvent ainsi parfaitement mélangés.

On pose alors les définitions suivantes:

– La transformation est dite fortement mélangeante si, pour tout couple de parties mesurables A et B de 行, on a:

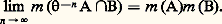– La transformation est dite faiblement mélangeante si, pour tout couple de parties mesurables A et B de 行, on a:

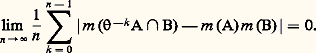Il est clair que toute transformation fortement mélangeante est, a fortiori, faiblement mélangeante et que toute transformation faiblement mélangeante est, a fortiori, ergodique.

La condition de mélange faible est particulièrement intéressante du point de vue analytique. Reprenons l’opérateur T défini au chapitre 2. On peut définir le spectre de T (cf. théorie SPECTRALE). Disons que T a un spectre continu si 1 est la seule valeur propre de T et de plus valeur propre simple. On peut alors prouver que est faiblement mélangeante si, et seulement si, T a un spectre continu.

4. Systèmes dynamiques

On ne donnera pas de définition générale et on se limitera aux systèmes ( 行, m , ) ayant les propriétés énoncées au début du paragraphe 2 en renvoyant à l’article SYSTÈMES DYNAMIQUES. On appelle un tel triplet 崙 = ( 行, m , ) un système dynamique. Soit 崙 = ( 行 , m , ) un autre système dynamique. On dira que 崙 est image homomorphe de 崙 s’il existe une injection mesurable 﨏: 行行 telle que 﨏 獵 = 獵 﨏 et m = 﨏(m ). Si 﨏 est bijective et si chacun des systèmes 崙 et 崙 est image homomorphe de l’autre par 﨏 et 﨏^-1, 崙 et 崙 sont dits spatialement isomorphes . Cela étant, on peut poser la question suivante: Deux systèmes dynamiques donnés sont-ils isomorphes? Pour y répondre, il est bon de rechercher les invariants d’un système dynamique 崙, c’est-à-dire les objets attachés à 崙 qui ne varient pas dans un isomorphisme spatial. Dans le chapitre 2, on a associé à la transformation un opérateur unitaire T dans L²(m ). Il est alors facile de vérifier que les valeurs propres de T sont des invariants de 崙.

Un autre invariant fondamental des systèmes dynamiques est l’entropie ou invariant de Kolmogoroff-Sinaï qui peut se définir de la façon suivante: Désignons par 﨑 la fonction réelle continue et positive sur [0, 1], telle que 﨑(x ) = 漣 x lg x , pour 0 麗 x 諒 1; à toute partition mesurable finie:

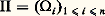de 行, faisons correspondre le nombre H( 刺) défini par:

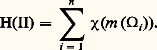On observe que, pour tout entier k ,

est une autre partition de 行 et l’invariance de la mesure entraîne que:

La fonction 﨑 est concave et l’on en déduit, pour deux partitions 刺 et 刺 , que: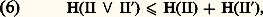

en notant 刺 鈴 刺 la partition engendrée par 刺 et 刺 . Les propriétés (5) et (6) permettent de prouver l’existence de la limite:

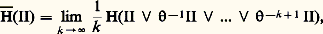et aussi l’inégalité:

On pose alors:

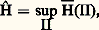la borne supérieure étant prise sur l’ensemble des partitions mesurables finies 刺 de 行. Le nombre H (éventuellement + 秊) est l’entropie du système 崙. Ajoutons que cette notion est très voisine de celle qui est utilisée par Boltzmann dans la théorie cinétique des gaz et qu’elle a été l’objet de profonds et difficiles travaux de Sinaï qui, par là, a fait un pas important vers la solution du problème fondamental de la théorie ergodique (cf. chap. 1).

Pour terminer, donnons un exemple. Soit A =a ¹, a ², ..., a ⁿ un ensemble à n éléments; munissons-le de la topologie discrète et de la mesure de probabilité équirépartie:

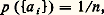pour i = 1, 2, ..., n . Posons 行 = A^Z; chaque élément de 行 est une suite infinie dans les deux sens 諸 = (..., 諸^-1, 諸⁰, 諸¹, ...) d’éléments de A. Avec la topologie produit, 行 est un espace compact sur lequel agit la transformation définie par ( 諸)^j = 諸^j+1 , appelée shift-transformation. Si m désigne la probabilité produit sur 行, le triplet ( 行, m , ) est un système dynamique qui joue un rôle important en théorie de l’information. Choisissons la partition:

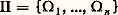où 行 ⁱ = 諸| 諸⁰ = a ⁱ. Il est clair que m ( 行 ⁱ ) = 1/n et que H( 刺) = log n . On peut alors prouver que l’entropie H de ce système dynamique est log n , ce qui montre en particulier que les systèmes obtenus pour des valeurs distinctes de n ne sont pas spatialement isomorphes.

5. Théorie ergodique, probabilités et potentiels

Les problèmes de convergence qui sont abordés au chapitre 2 concernent l’opérateur T: f 料 Tf = f 獵 agissant dans L¹(m ) ou L²(m ). Cet opérateur possède les propriétés qui suivent:

a ) T est linéaire;

b ) T est positif: f 閭 0 輦 Tf 閭 0;

c ) T est une contraction, c’est-à-dire: face=F0019 瑩Tf 瑩¹ 諒 瑩f 瑩¹ pour tout f 捻 L¹(m ).

On peut aussi considérer de façon plus générale des endomorphismes de l’espace (réel) L¹(m ) possédant les propriétés précédentes et non nécessairement induits par des transformations ponctuelles . De tels opérateurs se présentent naturellement dans la théorie des processus markoviens. Ils sont définis à partir d’un noyau N: 行 憐 龍 雷⁺ (face=F0021 龍 désignant la tribu des ensembles mesurables de 行) où l’on suppose que l’application partielle 諸 料 N ( 諸, A) est mesurable pour A constant et que l’application A 料 N( 諸, A), 諸 étant fixé, est une probabilité (ou une sous-probabilité) sur 龍. À tout f 捻 L¹ on associe la mesure réelle 猪 ^f sur ( 行, 龍) par la formule:

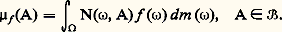Si l’on suppose que 猪^f est absolument continue par rapport à m , et cela quel que soit f , la densité Tf = d 猪^f dm est la transformée de f par T. La vérification des propriétés a , b et c est immédiate.

Le théorème ergodique général, établi en 1960 par Chacon et Ornstein, pour une contraction positive T affirme que: Quelles que soient les fonctions intégrables f et g , g 閭 0, l’expression:

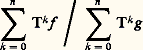tend presque partout vers une limite finie sur l’ensemble:

Chacon a, de plus, explicité cette limite. Cet important théorème, faisant suite à des travaux de Doob et de E. Hopf, a été aussi prouvé par J. Neveu par des méthodes probabilistes.

Le lien avec la théorie du potentiel découle de recherches faites par A. Brunel, par P. A. Meyer et par Ackoglu qui ont utilisé le lemme suivant, appelé lemme ergodique maximal.

Soit f 捻 L¹ (réel) et A 捻 龍 tel que:

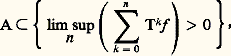alors:

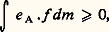en désignant par e ^A le potentiel d’équilibre de A, relativement au noyau transposé ^t T de T.

L’opérateur ^t T qui agit dans L 秊 se définit par dualité: Quels que soient f 捻 L¹ et g 捻 L 秊,

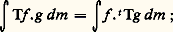la fonction e ^A est, en gros, la plus petite fonction ^t T 漣 sous-invariante (^t Te ^A 諒 e ^A) qui majore 1^A.

On a voulu montrer comment la théorie ergodique s’est développée et ramifiée à partir du problème fondamental posé par l’hypothèse ergodique. Il n’était pas possible de résumer ici d’autres travaux difficiles, par exemple ceux qui concernent les groupes ou les semi-groupes de transformations ou d’opérateurs.

Encyclopédie Universelle. 2012.